CS173: Intro to Computer Science - Public-Key Cryptography (100 Points)
Assignment Goals
The goals of this assignment are:- To implement mathematical theory in the Java programming language
- To apply library functionality from external jar files and build upon existing functionality
- To implement algorithms that iterate over characters in a
Stringand over elements in an array
Background Reading and References
Please refer to the following readings and examples offering templates to help get you started:- Mini Crypto Activity
- Strings Activity
- Iteration Activity: For Loops
- Iteration Activity: While Loops
- Iteration Activity: Do Loops
The Assignment
This assignment is adapted from Prof. Mongan’s assignments in communications and introductory cryptography [1, 2, 3], and from the CS Unplugged Public Key Encryption lesson module [4].
RSAMath Library
The mathematics functions used in this assignment are provided in the jar file library rsamath.jar. First, download the jar to a location you’ll remember. To use this jar, after creating a Java project in NetBeans as usual, right-click on the project in your left project navigation pane (you can click the Window menu and select Projects if you don’t see this), and click Properties, as shown:
Click the Libraries category on the left side of the window that appears. Then click, the + sign next to the word Classpath, and click Add JAR/Folder, as shown:
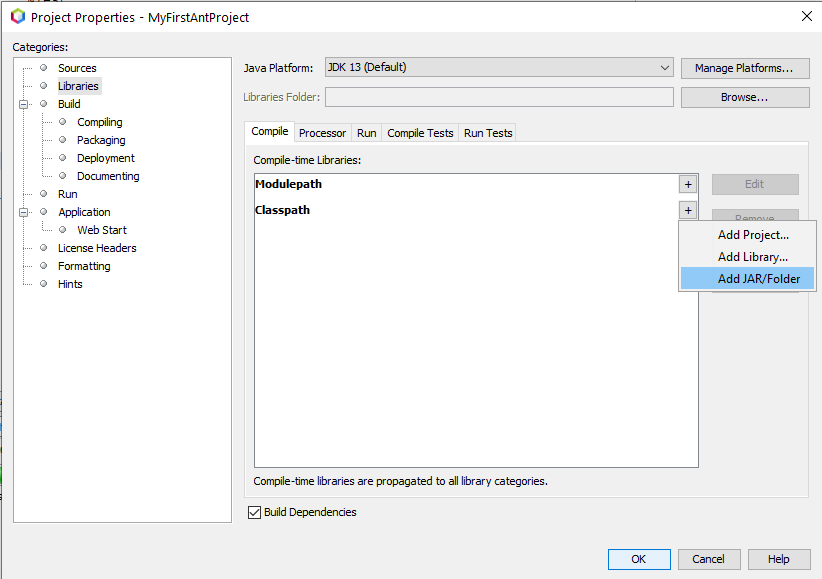
Finally, navigate to the jar file you downloaded earlier, and double click on it to add it to your project. Click OK to close the window, and you’re done!
To see which functions are available in the RSAMath library, see the Javadoc. The RSAMath class is implemented in the cs4hs11.rsalibrary package, which you can import in your program. If you get an error indicating that the RSAMath methods are not static, you can create an RSAMath object and then call the functions on the resulting object. Here is a listing of the methods you’ll find in this library:

Step 1: Encrypting Characters Using A Public/Private Key that We Create
Generate a Public/Private Key Pair
Write a function to generate a public and private key pair and print these to the screen. Write a main() function to test this functionality.
A number N is prime if no number from 2 to N-1 divides evenly into it. That is, \((N (mod \; k)) \ne 0\) for all \(k \in [2, N-1]\).
Once you generate those prime numbers (let’s call them A and B), you can generate your public key (E, C) and private key (D, C). Recall that the value C is shared between the public and private key, and that E and C are made available to others so that they can encrypt data to you. Your private key (D, C) is needed to decrypt those values, so you must keep the value D a secret!
To generate your public key:
- Choose two prime numbers A and B. Make these prime numbers at least 2 digits in length, but no more than 3 digits. In practice, the values are much larger, but this is a demonstration.
- Compute \(C = AB\). Since the ASCII table contains 128 entries (numbered 0 through 127), C should be larger than 127, so that all these characters can be represented. If you send messages with characters from the extended ASCII table, C should be greater than 255.
- Compute \(M = \phi(C)\) by computing
(A-1)*(B-1). This will be equal to the result of theRSAMath.totient(C)method if your values of A and B are prime. - Compute E, a value co-prime to M. The
RSAMath.coprime(M)method can help you do this. - Compute D, the modular inverse of \(E (mod \; M)\). The
RSAMath.mod_inverse(E, M)method can help you do this.
Here is an example:
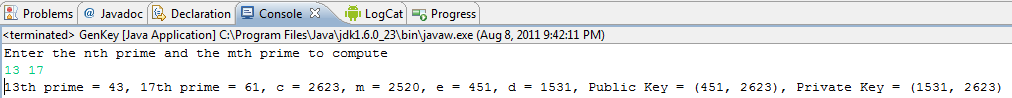
So, to get started, you can compute E as follows:
// do this import at the very top
// import cs4hs11.rsalibrary.RSAMath;
long A; // assign this to a prime number, perhaps from the Scanner or by computing one via a function
long B; // assign this to a prime number, perhaps from the Scanner or by computing one via a function
long C = A*B;
RSAMath rsa = new RSAMath();
long M = (A-1)*(B-1); // equal to rsa.totient(C), but much easier to compute!
long E = rsa.coprime(M);
Step 2: Communicating Secret Messages to a Partner Using Only Their Public Key
Now, write a program to accept your partner’s public key, and your private key. You can exchange keys via email, on Teams, or on the board. Accept a String parameter, and for each character in the String, obtain its ASCII value and encrypt it with your partner’s public key. Send those encrypted values to your partner.
Encrypting a Message to Your Partner Using Their E and C Key Values
Given a public key (E and C) as parameters, write a function to encrypt a given value, and return the encrypted value. Print this value to the screen.
Here is an example:
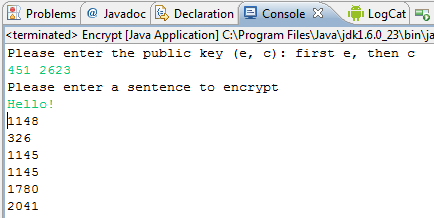
The RSAMath.endecrypt(X, E, C) function will help you to do this, by encrypting the value X using the encryption key E and C.
Your loop to obtain each character from the String will look something like this:
String msg = "This is a secret message!";
for(int i = 0; i < msg.length(); i++) {
// get each character from the string - the first one will be the letter T, followed by h, and so on...
char x = msg.charAt(i);
// TODO: encrypt this character and print the encrypted value to the screen
}
Each encrypted value X will be the ASCII value of each character in a String. You can iterate over the characters of the string, and obtain a char value representing each character in the loop. A char is really an integer whose value is the ASCII value of that character. So, you can obtain the numeric ASCII value of the character by casting the char to a long (a long is a whole number like an int, but it is double the size of an int):
long asciiX = (long) x; // where c is a char
Decrypting a Message from Your Partner Using Your D and C Key Values
Similarly, accept a private key (D and C) as parameters, write another function to decrypt a given value, and return that decrypted value. Print it to the screen as well.
The procedure is similar to that used to encrypt a value. The RSAMath.endecrypt(X, D, C) function will help you to do this, by encrypting the value X using the encryption key E and C.
Here is an example:
What do you notice about the encryption and decryption functions you just wrote? (Click to reveal)
They're exactly the same! They only differ in the input parameters (what values are used for the keys). This is because the mathematics results in the computation of the modular inverse of the value. The same function can be used on two different problems!Given a set of integers that are values encrypted by your partner using your public key, write a program that decrypts each of those values (using a loop!) and decrypt to the original secret message. Decide on a way to determine when you are finished so that you exit the loop nicely. Write down how you decided to do this! For example, you can read each encrypted long value from the user keyboard using the Scanner, and enter a negative number to indicate that you have finished reading. Continue reading and decrypting characters in a loop while the input is not negative!
The procedure to do this is similar to that used to encrypt each character, except that the value to be decrypted is the encrypted value of the ASCII value used before, and the key is the private key (D, C) associated with the public key that was used to encrypt it. You can cast the ASCII value you obtain as a long back to a char, and either print it or concatenate it with a String.
Hint: You will encrypt data using your partner’s public key values E and C, and decrypt usnig your own private key values D and C. The values of C will not be the same, since they are for two different keys (your partner’s and your own)!
When you decrypt a secret message using your own private key, you’ll get back a long, as follows:
long decrypted = RSAMath.endecrypt(encrypted, D, C);
You can convert the long back to a char for printing as follows:
char decryptedChar = (char) decrypted;
Test the Public/Private Key Pair by Encrypting and Decrypting Using Your Own Public and Private Key
Write test cases that encrypt values using your public key, and decrypt them using your private key, and assert that the final decrypted value matches your original input. Also try encrypting with your private key and decrypting with your public key, to ensure that the keys are proper inverses of one another.
Step 3: Breaking Someone’s Private Key Using Only Their Public Key
Going back through the RSA algorithm, how did you compute your private key from your public key? Since they are modular inverses of one another, you could compute the modular inverse of your partner’s public key (E and C) to obtain their private key D.
Why is this too difficult to do in practice, when the key values are much larger?
Since these are small keys, you can compute the Totient of C (\(M = \phi(C)\)) directly, or by computing \(M = (A-1)(B-1)\). Notice that these are essentially the same problem, since counting the values that are coprime to a number is effectively the same as searching for the two values that are not coprime - the factors A and B.
Write and test a program to accept a public key. To do this, compute your partner’s private key from their public key, and test that you can obtain your own private key given your public key. Print the private key to the screen and verify that it is correct with your partner. This program should only accept E and C, the public key, as inputs.
Here is an example:

Summary
As a summary, here is what to do. You might want to write separate programs (projects) for each of these, and export and submit each of them. It’s up to you!
- Generate a key to share with the class. Share your
EandCpublic key with the class, but keep yourDprivate key value a secret that you will use later! - Use someone else’s public key (
EandC) to encrypt a secret message to them, one character at a time. You can loop over the characters of aStringto do this. Share your encrypted numeric values with that person. - When someone shares a message with you, use your own private key (
DandC) to decrypt them to characters, one by one, and print them to the screen. What message did you get? Note that thisCis different than the one you used to encrypt something to your classmate in the prior step: you used theirCvalue instead! Here, you are using your own value ofC. - Take someone’s public key (
EandC) and computeMandDfrom it. Did it match their private key? Why is this hard to do with actual public keys on the internet?
Extra Credit (15 Points)
Implement the RSAMath functions
Create your own versions of each of the functions in the RSAMath library given to you, and use those instead in your programs!
Exporting your Project for Submission
When you’re done, write a README for your project, and save all your files, before exporting your project to ZIP. In your README, answer any bolded questions presented on this page. Here is a video tutorial describing how to write a README for your project, and how to export it.
A Note About Export Controls
Some governments, including the United States, have export controls on cryptographic technologies.
-
William M. Mongan. 2012. An integrated introduction to network protocols and cryptography to high school students (abstract only). In Proceedings of the 43rd ACM technical symposium on Computer Science Education (SIGCSE ’12). Association for Computing Machinery, New York, NY, USA, 664. DOI:https://doi.org/10.1145/2157136.2157364 ↩
-
William M. Mongan. 2011. Networking Applications, Protocols, and Cryptography with Java. Google CS4HS Workshop at the University of Pennsylvania, Philadelphia, PA. ↩
-
William M. Mongan. 2012. Networking Applications, Protocols, and Cryptography with Java. Tapia Workshop at the University of Pennsylvania, Philadelphia, PA. ↩
-
Bell, Witten, and Fellows. 1998. Computer Science Unplugged - Public Key Encryption. Available at https://classic.csunplugged.org/public-key-encryption/ ↩
Submission
In your submission, please include answers to any questions asked on the assignment page in your README file. If you wrote code as part of this assignment, please describe your design, approach, and implementation in your README file as well. Finally, include answers to the following questions:- Describe what you did, how you did it, what challenges you encountered, and how you solved them.
- Please answer any questions found throughout the narrative of this assignment.
- If collaboration with a buddy was permitted, did you work with a buddy on this assignment? If so, who? If not, do you certify that this submission represents your own original work?
- Please identify any and all portions of your submission that were not originally written by you (for example, code originally written by your buddy, or anything taken or adapted from a non-classroom resource). It is always OK to use your textbook and instructor notes; however, you are certifying that any portions not designated as coming from an outside person or source are your own original work.
- Approximately how many hours it took you to finish this assignment (I will not judge you for this at all...I am simply using it to gauge if the assignments are too easy or hard)?
- Your overall impression of the assignment. Did you love it, hate it, or were you neutral? One word answers are fine, but if you have any suggestions for the future let me know.
- Any other concerns that you have. For instance, if you have a bug that you were unable to solve but you made progress, write that here. The more you articulate the problem the more partial credit you will receive (it is fine to leave this blank).
Assignment Rubric
| Description | Pre-Emerging (< 50%) | Beginning (50%) | Progressing (85%) | Proficient (100%) |
|---|---|---|---|---|
| Algorithm Implementation (60%) | The algorithm fails on the test inputs due to major issues, or the program fails to compile and/or run | The algorithm fails on the test inputs due to one or more minor issues | The algorithm is implemented to solve the problem correctly according to given test inputs, but would fail if executed in a general case due to a minor issue or omission in the algorithm design or implementation | A reasonable algorithm is implemented to solve the problem which correctly solves the problem according to the given test inputs, and would be reasonably expected to solve the problem in the general case |
| Code Quality and Documentation (30%) | Code commenting and structure are absent, or code structure departs significantly from best practice, and/or the code departs significantly from the style guide | Code commenting and structure is limited in ways that reduce the readability of the program, and/or there are minor departures from the style guide | Code documentation is present that re-states the explicit code definitions, and/or code is written that mostly adheres to the style guide | Code is documented at non-trivial points in a manner that enhances the readability of the program, and code is written according to the style guide, and each function contains relevant and appropriate Javadoc documentation |
| Writeup and Submission (10%) | An incomplete submission is provided | The program is submitted, but not according to the directions in one or more ways (for example, because it is lacking a readme writeup or missing answers to written questions) | The program is submitted according to the directions with a minor omission or correction needed, including a readme writeup describing the solution and answering nearly all questions posed in the instructions | The program is submitted according to the directions, including a readme writeup describing the solution and answering all questions posed in the instructions |
Please refer to the Style Guide for code quality examples and guidelines.