CS173: Intro to Computer Science - Drawing Faces (100 Points)
Assignment Goals
The goals of this assignment are:- To write a function that accepts parameters and draws a figure on the screen according to those parameters
- To explore the composition of colors in the RGB color system
Background Reading and References
Please refer to the following readings and examples offering templates to help get you started:The Assignment
Getting Started with the StdDraw Library
Adding the Princeton stdlib Library to Your Project
The edu.princeton.cs.algs4.StdDraw class contains a library that will draw polygons and other shapes on a window. The coordinates of this window are assumed to range from [0, 1]. This class is contained in the algs4.jar file provided by Robert Sedgewick.
First, download the jar to a location you’ll remember. To use this jar, after creating a Java project in NetBeans as usual, right-click on the project in your left project navigation pane (you can click the Window menu and select Projects if you don’t see this), and click Properties, as shown:
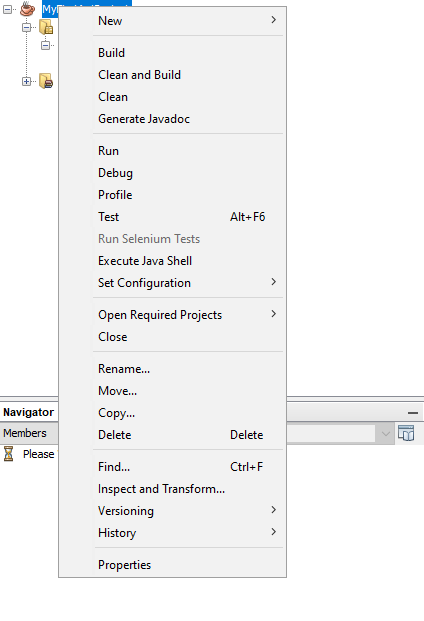
Click the Libraries category on the left side of the window that appears. Then click, the + sign next to the word Classpath, and click Add JAR/Folder, as shown:
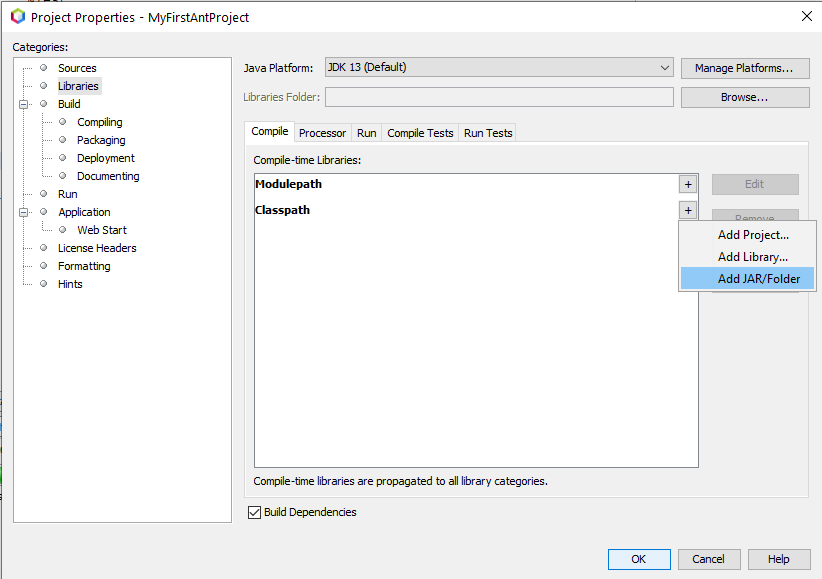
Finally, navigate to the jar file you downloaded earlier, and double click on it to add it to your project. Click OK to close the window, and you’re done!
In your program, you can add the following import line at the top:
import edu.princeton.cs.algs4.*;
Background Information: Basic Drawing Functionality
You can draw arcs and circles using the following methods, once you add the jar to your project, by calling one of these functions from your program. This is just for your reference - do not include this code in your project, as it is already present in the jar file you imported!
// DO NOT COPY THIS PART OF THE CODE - THIS IS JUST A REFERENCE!
// These are like Math.pow() - functions that the jar file provides
// now you have functions called StdDraw.circle and StdDraw.arc, that
// look like the below functions.
// Assumption: the edu.princeton.cs.algs4 package is imported in this file with
// import edu.princeton.cs.algs4.*;
//... then inside your class, and inside main(), you can call these functions:
// x and y are the center coordinates of the circle
// radius is the radius of the circle (or the circle traced by the arc)
// angle1 and angle2 are the angles traced by the arc from the starting and ending points, respectively
// ... where 0 is the 3 o'clock position, and 90 is 12 o'clock, 180 is 9 o'clock, and 270 is 6 o'clock.
// ... angle1 is where to start tracing the circle, and angle2 is where to stop.
public static void arc(double x, double y, double radius, double angle1, double angle2)
public static void circle(double x, double y, double radius)
For example, you can draw a circle centered at the middle of the window, with a radius of 0.5 (since the window has dimensions 1 by 1, this circle will take up the whole window):
StdDraw.circle(0.5, 0.5, 0.5); // put this inside your public static void main() function.
StdDraw.arc(0.5, 0.5, 0.4, 90, 270); // this draws a circle inside, but only a semi-circle
Here is a list of all the functions provided by StdDraw, in addition to the circle and arc functions given above.
Part 1: Drawing Faces
Using the StdDraw methods and examples above, try drawing a “happy face” at the center of the window. Recall that the coordinate plane of the window on the x and y axes ranges from 0 to 1, so your coordinates should always be in this range. Your happy face should have:
- a circle for a face
- circles for eyes inside the face circle
- an arc for the nose
- an arc for the smile
For fun, you can add some eyebrows with arcs, too!
Creating a Function to Encapsulate Your Face Drawing Functionality
Now, create a function called drawHappyFace that draws a face centered at coordinates given as function parameters.
Instead of hard-coding the x, y, and radius values for your face, calculate them based on the input parameters. For example, your eyes might have a y value that is equal to the given y parameter plus or minus one-half the radius (this is just an example - feel free to play with the values like this and see where the eyes end up for yourself!). I suggest hard-coding values at first to see the relationship between x, y, and radius, and the ultimate placement of the facial features.
As an example, suppose you wish to draw a “left eye” that is halfway between the left edge of the face circle, and the center of the circle. The x-coordinate of the center of the eye would be equal to the center of the face circle minus half the radius of the face circle. The radius of the eye might be, for example, some fraction of the radius of the face circle (perhaps 10%). You can compute variables for the x, y, and radius of the circles and arcs based upon the x, y, and radius of the face circle itself. This is a trial-and-error process, and there is no specific correct answer: play with the values and see where the elements are drawn. Sketching this on paper and labeling the x and y points is a helpful idea.
Calling the Function Multiple Times to Draw Several Figures
From your main function, call your drawHappyFace function at least 3 times, with different parameters, to draw at least 3 faces on different parts of the screen. The faces should not overlap on the screen, and the elements within each face should appear inside the face circle.
Part 2: Changing the Color
Background: Color Coding
To create the color codings, the proportion of votes cast for each of (up to) three candidates is converted into a RGB color. An RGB color is defined by a “tuple,” or collection of values: each value in this 3-tuple represents the proportion of red, blue, and green to be mixed in to the color shown. This is called a 3-tuple because there are three values in the tuple (the red, blue, and green proportion).
We will use 24-bit color in this example, meaning that each of the three values (red, green, and blue) in the tuple can be represented with an 8-bit value.
How many different values can you represent with an 8-bit value? In other words, how many different pure "red" colors are there? There will be an equal number of pure "blue" and pure "green" values as well. (Click to reveal)
Since each of the 8 bits is a binary bit value (0 or 1), there are two possibilities for each of the eight bit fields. Thus, there are \(2^{8}\) different values that can be represented using an 8-bit entry, or 256 distinct shades of pure red, pure blue, or pure green. This includes the colors black (a value of 0) and white (a value of 255).How many different values can you represent with a 24-bit value? In other words, how many different colors can we work with in total? (Click to reveal)
There are \(2^{24}\) or approximately 16 million colors that we can represent as combinations of the 256 possible red values, 256 possible blue values, and 256 possible green values. This is the same as combining three entries of up to 256 possibilities each (the 256 reds, 256 greens, and 256 blues), or \(256^{3}\). By the law of exponents, \(2^{24} = (2^{8})^{3} = 256^{3}\).The color wheel below from Wikipedia shows some example color mixtures. These values are in hexadecimal, so they range from 0x00 to 0xff for decimal values 0 to 255. Here is a guide from Khan Academy to number systems and converting between hexadecimal, binary, and decimal.

Setting the Color
You can set the color of your face using integers for red, green, and blue, as follows:
// Don't forget to add the import if you get an error here! You can click on the light bulb in NetBeans and select the Import option
Color color = new Color(red, green, blue);
StdDraw.setPenColor(color);
Modify your drawHappyFace function to accept three additional int parameters for red, green, and blue, and set the color in the beginning of your function so that the face draws in the color you specify (each color is a mixture of red, green, and blue, with values ranging from 0 to 255). Modify your main function to provide red, green, and blue values of your choosing to each of your calls to drawHappyFace: use different colors each time!
You can visit this page to identify red, green, and blue values for your favorite colors.
Exporting your Project for Submission
When you’re done, write a README for your project, and save all your files, before exporting your project to ZIP. In your README, answer any bolded questions presented on this page. Here is a video tutorial describing how to write a README for your project, and how to export it.
Design Questions to Help You Begin
Please answer the following questions in your README file before you begin writing your program.- What is an x, y, and radius value that you might use to draw the left eye on a face whose
x = 0.2,y = 0.3, andradius = 0.2? How about the right eye? - What is an x, y, and radius value that you might use to draw the left eye on a face whose
x = faceX,y = faceY, andradius = faceRadius? How about the right eye? In other words, how did you compute the x, y, and radius values for the eyes, given the values for the face?
Submission
In your submission, please include answers to any questions asked on the assignment page in your README file. If you wrote code as part of this assignment, please describe your design, approach, and implementation in your README file as well. Finally, include answers to the following questions:- Describe what you did, how you did it, what challenges you encountered, and how you solved them.
- Please answer any questions found throughout the narrative of this assignment.
- If collaboration with a buddy was permitted, did you work with a buddy on this assignment? If so, who? If not, do you certify that this submission represents your own original work?
- Please identify any and all portions of your submission that were not originally written by you (for example, code originally written by your buddy, or anything taken or adapted from a non-classroom resource). It is always OK to use your textbook and instructor notes; however, you are certifying that any portions not designated as coming from an outside person or source are your own original work.
- Approximately how many hours it took you to finish this assignment (I will not judge you for this at all...I am simply using it to gauge if the assignments are too easy or hard)?
- Your overall impression of the assignment. Did you love it, hate it, or were you neutral? One word answers are fine, but if you have any suggestions for the future let me know.
- Any other concerns that you have. For instance, if you have a bug that you were unable to solve but you made progress, write that here. The more you articulate the problem the more partial credit you will receive (it is fine to leave this blank).
Assignment Rubric
| Description | Pre-Emerging (< 50%) | Beginning (50%) | Progressing (85%) | Proficient (100%) |
|---|---|---|---|---|
| Algorithm Implementation (60%) | The algorithm fails on the test inputs due to major issues, or the program fails to compile and/or run | The algorithm fails on the test inputs due to one or more minor issues | The algorithm is implemented to solve the problem correctly according to given test inputs, but would fail if executed in a general case due to a minor issue or omission in the algorithm design or implementation | A reasonable algorithm is implemented to solve the problem which correctly solves the problem according to the given test inputs, and would be reasonably expected to solve the problem in the general case |
| Code Quality and Documentation (30%) | Code commenting and structure are absent, or code structure departs significantly from best practice, and/or the code departs significantly from the style guide | Code commenting and structure is limited in ways that reduce the readability of the program, and/or there are minor departures from the style guide | Code documentation is present that re-states the explicit code definitions, and/or code is written that mostly adheres to the style guide | Code is documented at non-trivial points in a manner that enhances the readability of the program, and code is written according to the style guide |
| Writeup and Submission (10%) | An incomplete submission is provided | The program is submitted, but not according to the directions in one or more ways (for example, because it is lacking a readme writeup or missing answers to written questions) | The program is submitted according to the directions with a minor omission or correction needed, including a readme writeup describing the solution and answering nearly all questions posed in the instructions | The program is submitted according to the directions, including a readme writeup describing the solution and answering all questions posed in the instructions |
Please refer to the Style Guide for code quality examples and guidelines.